MiquelFire's Blog
-
Environment is ready
And so, the Miquel of Fire had decided to embarked on a journey of creating game in a short 72 hour time span. Two nights before he would receive the rules he would need to follow, he did some prep work in the form of making sure his compiler setup of MSVC2013 works. After a few checks with the unstable Allegro 5.1.11 release, he got to a state where he deemed it good enough.
As he was getting ready for bed, he remembered some more prep work he wanted to get done, but was too tired to care, and it wasn't too complex in his mind to worry about being in a hurry to do it. He would log off his computer and go to bed, as he needed to go to his paid job in the morning.
-
Will be streaming
==Story mode break==
I'll be streaming at http://www.twitch.tv/miquelfire when I'm coding. As of now, I'm still trying to figure out a game for these rules. Having a hard time being creative. And my god, a rule I created was picked.
-
The quest for a game idea
Miquel of Fire wakes up, and eats breakfast. The contest had started by the time he finish, so he read them. The rules puzzled him greatly as he could not think of anything. After starting up his computer and the stream on the Twtch, all the while trying to think up something, he added a random number generator to his code base, as his last entry had issues with it.
And thus the quest for some idea to work with has begun. Will this be the end? Find out next time.
-
Quest for a name
Miquel of Fire has decided on a game to work on. However the name of the game is a bit of an issue.
He has decided to eat lunch for a bit, and will return later to flesh out the ideas of the game.
-
Some progress has been made
Thanks to a distraction that he knew would be long, but still ended up longer than he would of have like, Miquel of Fire has not only got a name for his game, but also a general layout for how the game will work. That distraction ended up taking away too much time for him to code.
As is the nature of the contest, he hacked away at some code he had the last time he did this trip. He's at a point where he needs code that would have to be created for the game he had set out to create.
He current plan is to get as far as possible with getting something working on getting visible progress before he has to go to sleep, but wants to get enough of the game done that he can spend most of Sunday fine tuning the game.
-
Game plan
Miquel of Fire made some minor changes in his design doc before he got on his computer. Instead of having water that is flammable, he would have some metal that is bouncy like rubber. As a result, he needed to change how he would put in particles in the game.
He sets off to make today a coding day.
-
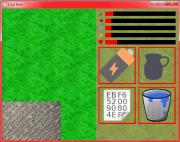
Some hard bit
Miquel spent some time working on the UI for the main part of the game people will be looking at. After many distractions, he finally has an image to show his work. Finally, he's at a state where future updates can have pictures!
He is glad he has a cat pillow he can use at times.
-
Miquel Supports Multiple Resolutions!
Miquel had forgotten to show off that his game is able to handle different resolutions. 640x480 might be the smallest however.
-
Meet Chip
Miquel next step was to have chip appear on the screen. While he hasn't yet started on the "AI" for chip, he at least wanted people to see him.
He also wanted any willing people to help if they want on anything by going to https://bitbucket.org/miquelfire/sh2015
He has yet to want to deal with switching to Git, as Mercurial is good enough for him. So that's a bit of a warning if you use those type of tools.
-
The heat is on!
Feeling pressured by time, Miquel has decided to switch to at least getting the other two rules he's been holding back on to at least have them completed. First thing first, the dialog system he planned on.
-
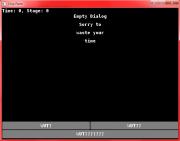
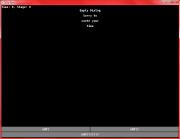
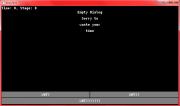
Dialog work underway
Miquel spent a little trial and error, but he has a dialog screen with three buttons. Now he just needs to test with the other three layouts, and have the buttons do stuff!!!
Note: Images already out of date, the message has been moved down.
-
Particles are a go
Miquel spent too much trial and error on it, but he has particles in his game. Miquel now just needs to set his sights on fulling the seedling rule.
-
Final entry
Miquel of Fire has completed his entry for the SpeedHack of 2015. And as such, this will be the last blog entry.
He has no plans to make any more versions of this game, though he might do some coding fixes for other platforms.